POS:V神：如何使用内积参数 (IPA) 进行数据可用性抽样（DAS）-ODAILY

当前的数据可用性抽样计划使用KZGcommitments完成。KZG承诺的优点是它们非常易于使用，并且具有一些非常好的代数性质：

一个评估证明具有恒定的大小，并且可以在恒定的时间内进行验证。

这里存在一种算法来计算所有证明，这些证明在O(N?log(N))时间内在N个单位根的每一个都会评估deg<N

您可以线性组合承诺以获得这个线性组合的承诺：com(P)+com(Q)=com(P+Q)

您可以线性组合证明：Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

第一点是良好的效率保证。第二点确保生成可以进行DA采样的blob很容易：如果生成所有证明需要O(N2)这么长的时间，则需要高度中心化的参与者或复杂的分布式算法才能使其准备好DAS。

第三点和第四点对于2D采样非常有价值，并且可以实现分布式区块生产者和高效的自我修复：

V神：ETH合并后Gas费可能低至0.002美元:金色财经报道，以太坊创建者Vitalik Buterin称，ETH合并后，Gas费可能低至0.002美元。要说明的是，合并后的Gas费下降包括汇总，可能在0.002美元至0.05美元之间。

此前消息，以太坊Goerli测试网已完成合并，Goerli是三个公共测试网中最后一个以太坊测试网，在此之后，主网合并预计将在9月底的某个时间发生。[2022/8/11 12:18:37]

区块生产者只需要知道原始的M承诺即可使用一种按照曲线的FFT来“扩展列”并生成在同一deg<M多项式上的2M承诺。

您不仅可以进行每行重建，还可以进行每列重建：如果列上的某些值和证明丢失，您可以执行FFT来恢复丢失的值和证明。

然而，KZG有一个弱点：它依赖于复杂的配对密码学和受信任的设置。配对密码学已经被研究使用了20多年，受信任的设置是N中的1个信任假设，N是数百名参与者，因此实践中的风险很高，作者认为继续使用KZG是完全可以接受的。但是，值得提出一个问题：如果我们不想支付KZG的成本，我们可以使用内积参数来代替吗？

V神：经过认证的去中心化区块链世界即将到来:金色财经报道，以太坊联合创始人兼核心开发人员Vitalik Buterin针对Reddit社区的《我对web3的第一印象》话题回复称，我认为经过认证的去中心化区块链世界即将到来，而且比许多人想象的更接近于此。当然，所有这些技术都有可能建立起来，而很多人不会关心。但我比较乐观。用户通常接受开发者给出的默认设置，而且很多开发者确实真正关心去中心化和不可信任的问题（而运行中心化信任节点的法律问题越来越多，会促使他们更加关心）。用户今天拒绝的去中心化选项（例如，运行一个完整的节点）在今天确实是相当困难，所以用户坚持使用更中心化的选项是可以理解的，至少他们可以轻松使用。这里列出的建议都没有那么困难，甚至运行一个完整的节点本身也会随着时间的推移变得更容易和更便宜。因为像无状态和历史过期的想法开始发挥作用，所以我看不出为什么未来需要像今天这样的技术原因。[2022/1/9 8:35:19]

有关IPA的解释，请参阅这篇文章的前半部分。

声音 | V神：自2014年以来，PoW不比PoS更平等:V神在推特中称，自2014年以来，PoW不比PoS更平等。对PoS的51%攻击不是无法恢复的，因为可以使用用户激活软分叉（UASF）的方法解决。PoS的安全性属于归纳论证，是完全合理的。另外，PoS和PoW的资源消耗不相同，PoW需要永久投资，PoW ASIC的寿命只有大约2年且运营成本很高，而PoS则更接近纯资本支出。[2019/12/1]

IPA具有以下特性：

评估证明具有对数大小，可以在线性时间内验证

没有已知的有效的多重证明生成算法。

承诺是椭圆曲线点，您可以像KZG承诺一样将它们线性组合

没有已知的线性组合证明的方法。

因此，我们保留了一些属性，也丢失了一些属性。事实上，我们失去的足够多，以至于我们生成、分发和自我修复证明的“当前方法”不再可能。这篇文章描述了一种替代方法，虽然有点笨拙，但仍然可以实现目标。

声音 | V神：有些举措看起来很浪费，但实际上是出于防御目的:在今天早上的Dragonfly Crypto Summit上，以太坊创始人V神表示：“我们做的很多事情看起来很浪费，但实际上是防御性的，比如多客户端的实现，这让我们能够挺过2016年的上海Dos攻击。”[2019/10/14]

一种替代方法

首先，我们生成一棵证明树，而不是为deg<N多项式生成2N独立证明，这看起来如下：

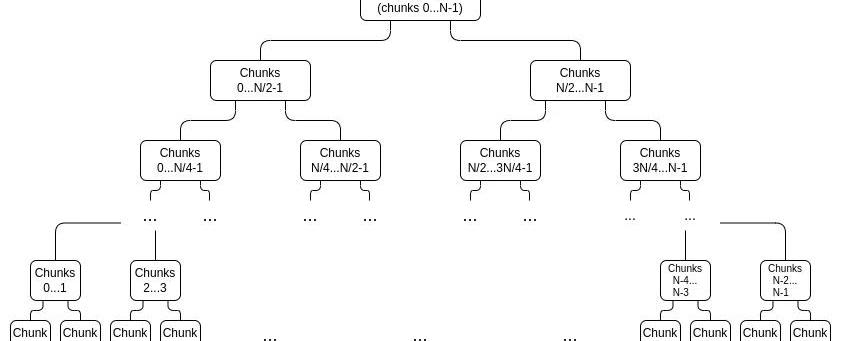
我们以评估形式解释数据，将其视为一个向量：

，其中多项式

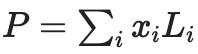
V神：我个人对跨链交流并不感冒:今日V神在王峰十问上表示：我知道有些团队正致力于跨链交流，但我个人对此并不感冒。[2018/6/22]

。

证明树中的每个节点都是对该部分数据的承诺，以及该承诺实际上“在界限内”的证明。例如，

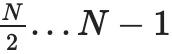
节点将包含承诺

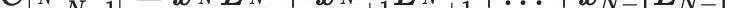
。将有一个IPA证明，

实际上是这些点的线性组合，没有其他点。

我们生成两棵树，第一棵用于

，第二棵用于

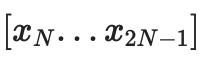
，对一条数据的“完整”承诺由C和C组成。为了证明一个特定的值xi，我们只需提供一个对列表，涵盖整个范围0...N?1或N....2N?1，不包括i，以及一个i不属于的顶级承诺是正确构建的证明。例如，如果N=8且i=3，则这个证明将包含C、C2、C及其证明，以及一个C被正确构造的证明。该证明将通过验证各个证明并检查承诺加起来是否构成完整承诺来进行验证。

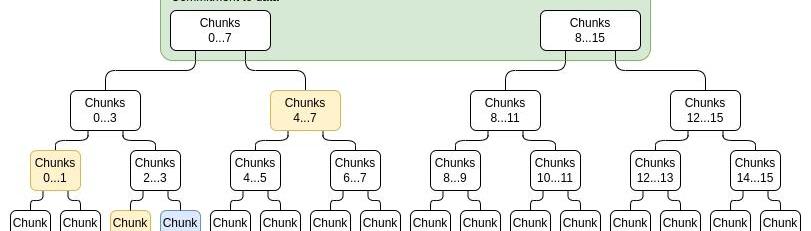
蓝色：chunk3，黄色：chunk3的证明。

注意，为了提高效率，每个chunk不需要是一个单独的评估；相反，我们可以裁剪树，例如一个chunk是一组16个评估。鉴于证明的组合大小无论如何都会比这大，像这样使chunk变大，我们损失很少。

生成这些证明需要O(N?log(N))时间。验证证明需要O(N)时间，但请注意，可以批量验证许多证明：验证IPA的O(N)步骤是椭圆曲线线性组合，我们可以使用随机线性组合检查其中的许多。每个证明仍然需要O(N)场域操作，但这只需要<1毫秒。

扩展：扇出出大于2

我们可以有一个更高的扇出，而不是每一步都有2扇出，例如8扇出。每个承诺我们将有7个证明，而不是每个承诺一个证明。例如，在底层，我们将有一个证明{1,2,3,4,5,6,7}，{0,2,3,4,5,6,7}，{0,1,3,4,5,6,7}等。这将总证明生成工作增加了

，但它将证明大小减少了3倍。

证明大小

假设我们正在处理大小为32的N=128chunk和一个(4x,4x,8x)的扇出。单个分支证明将包含3个IPA，总大小为2?(7+9+12)=56个曲线点加上chunk的512字节。今天256字节或512字节chunk拥有48字节证明。

生成证明总共需要2?8192?(3?2+7)次曲线乘法，或总共~212992次乘法。因此，这需要一台功能强大的计算机快速完成，或者需要一个分布式过程，其中不同的节点专注于为不同的chunk。

验证证明很容易，因为可以批量验证证明，并且只完成一个椭圆曲线乘法。因此，它不应该比使用KZG证明慢很多。

自我修复

无法逐列有效地进行自我修复。但是我们能否避免要求单个修复拥有所有数据？

假设单行完全丢失。很容易使用任何列来重建该列中缺失行中的值。但是如何证明呢？

最简单的技术是加密经济学：任何人都可以简单地发布一个声明一个值的债券，然后有人可以将该声明与证明不同值的分支证明一起使用，以削减该验证者。只要有足够的合法声明可用，该行子网上的某个人就可以将声明组合在一起并重建承诺和证明。甚至可能要求验证者针对分配给他们的样本索引发布此类声明。

一种没有加密经济学但在技术上更复杂且速度更慢的替代方案是传递沿该列的值的M分支证明，以及证明正确验证的Halo式证明。

标签：POSPOW以太坊COMPOSSempowr blue以太坊最新价格行情昭Buying.com

狗狗币最新价格热门资讯