PLO:密码专栏 | 超强进阶：PLONK VS Groth16（下）

前言

本篇是“PLONKVSGroth16”的下篇，在上篇中我们对PLONK作了简要介绍，分析了PLONK和Groth16算法在「可信验证」和「约束构建」上的异同。那么，接下来让我们一起看看在后续的「证明生成」和「验证阶段」两者将有怎样的差异，以及整体上的性能区别。

证明生成

对于程序qeval,prover需要证明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5

在上篇中我们已经介绍了PLONK的约束形式：门约束与线约束。继续使用之前的例子，约束意味着零知识证明系统将这个问题约束成了一组格式固定的数学表达式，即问题描述等价于约束描述。而如果证明者真的知道这个问题的答案，将答案和计算中的中间参数代入约束表达式，这个组表达式必将是成立的。反之，如果该Prover提供的一组解无法使表达式成立，说明prover并不具备关于该问题解的知识。

这是最朴素的证明验证思路，可以将它看作是“锁”和“钥匙的配对“：该问题约束的构建类似于“打造门锁“，而针对该问题提供的一组解信息就是”一把开启门锁的钥匙“。显然，Prover可以举着自己的解交给验证者来验证。可是这违背了我们的零知识原则：Verifier不应该获取到Prover的隐私信息。

Chia发布v1.2.10版本，使用密码提高密钥安全性:10月26日消息，Chia发布v1.2.10版本，使用密码提高了密钥安全性，解决了在断电等事件中潜在节点数据丢失的问题。[2021/10/26 20:57:22]

那么有什么方法能在解锁的同时保护隐私信息呢？

这里我们用到一个简单的数学小技巧：减除，对此不太了解的读者可查阅文章最后的前置知识。在前文《超强进阶：PLONKVSGroth16》我们已经对从约束系统转化到多项式进行了详细的描述，在此我们不再赘述具体的转化过程，但需要重复的一点是：根据生成时使用的点值对，生成的多项式在这些点处的取值将恒为0。PLONK同理，此处我们给出两种算法的约束系统转化为多项式后的形式。

Groth16:

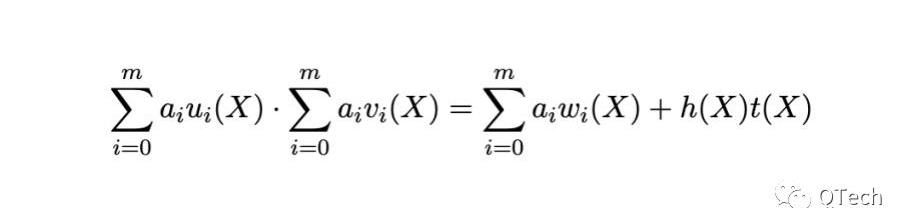
PLONK:?我们设门约束多项式为D(X)，线约束多项式为L(X)，那么PLONK的整个约束多项式将被表示为：

Nervos研究员论文被国际密码学顶会欧密会收录:近日，Nervos基金会密码学研究员Alan Szepieniec的论文《Transparent SNARKs from DARK Compilers》被国际密码学顶会欧密会收录，同时，Alan也受邀在该会议上发表了主题演讲。这项基础性的工作为零知识证明领域贡献了一种全新的无需Trusted Setup的通用工具，标志着 Nervos在2020年的研究工作又向前迈进了坚实的一步。

欧密会（Eurocrypt）是密码学中最著名的学术会议国际密码学协会所主办的三大旗舰会之一，在CCF推荐列表和 CACR列表中均为A类会议，密码学中最重要的文章一般都会在这三个会议中发布。Eurocrypt 2020是第39届密码技术理论与应用国际会议，首次在线上举行。[2020/5/18]

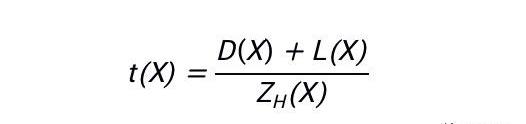
可以看到，两者都使用了减除的思路，也就是这里的h(X)和ZH(X)，其具体内容取决于构建约束多项式时取的点值。

央行：坚定不移推动金融领域密码应用:中国人民银行官方公众号4月15日发布文章《学习密码法 筑牢安全防线》，强调金融室国家重要的核心竞争力，密码是保障金融网络安全，促进资金融通、加强金融监管，以及支撑金融创新的关键技术和有效途径。密码在金融领域应用广泛，比如“数字签名”护航刷卡消费、商业密码助力网上银行转账。2020年是《中华人民共和国密码法》施行元年，也是密码工作创建90周年。中国人民银行提出六点要求：

1、提高站位坚决落实：坚定不移地推进金融领域密码应用，把各项部署落到实处；

2、规划引领战略融合：加强顶层设计和沟通协调，形成指导密码应用的发展规划；

3、顺应形势创新驱动：坚持问题导向，推动创新链、产业链、价值链的整合，实施密码优先发展战略；

4、分类施策全面推进：构建金融基础设施密码支撑体系，扩大金融领域的密码应用。

5、依法管理强化评估：加强金融行业密码应用的政策和标准制定，抓好密码应用安全性评估；

6、统筹推进形成合力：推动金融领域密码全面规范应用，建立健全金融领域网络密码保障体系。[2020/4/15]

证明与验证

同样在之前的文章中，我们可以看到Groth16的证明规模极小，只包含三个群元素A,B,C。然而，这样优雅的证明实现依赖于它的非通用可信设置，这也是Groth16的一大痛点。在Groth16中，证明方提供A，B，C，验证方基于可信设置提供的参数，构建一个配对验证等式。在验证过程中包含了三次配对操作，也就是对验证性能影响较大的耗时运算。Groth16的具体证明验证如下所示。

动态 | EOS在CoinMarketCap基本密码资产评分中排名第一:据引力观察消息，Coinmarketcap在他们的网站上添加了基本密码资产评分(FCAS)。FCAS是度量加密货币项目健康状况。EOS目前在FCAS排名第一，915分，其次是ETH和BTC。[2019/3/21]

Groth16证明：

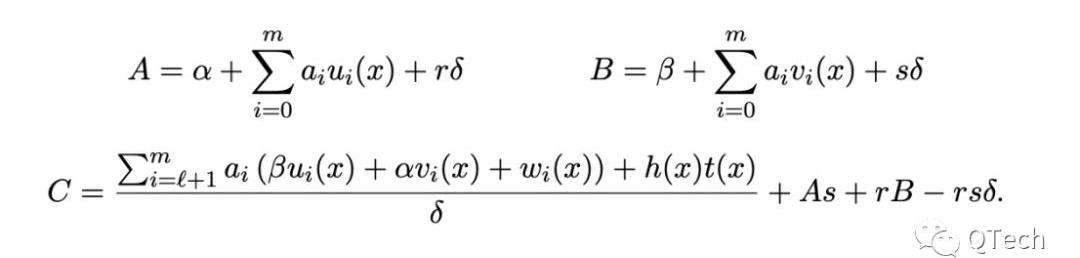
Groth16验证：

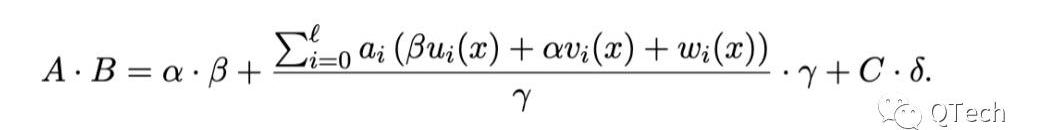
相比之下，PLONK的证明验证将会复杂得多，这也是使用通用可信设置付出的代价。从验证方角度看，由于可信设置参数缺少了包含问题具体内容，从而无法帮助其构建一些制约证明多项式的值。因此，如何固定住证明多项式的内容成为一个难题。PLONK使用的一个思路是引入Kate承诺。

声音 | 以太坊钱包MyCrypto创始人：用户密码设置是薄弱环节:针对Coinbase Wallet可在Google Drive或iCloud上备份私钥，以太坊钱包MyCrypto创始人兼首席执行官Taylor Monahan持观望态度。其表示：“无论加密强度如何，薄弱环节始终是用户选择的密码。用户无法生成足够复杂的密码，且习惯性使用单一密码。”其认为，“针对这些云存储提供商的攻击将会增加。”[2019/2/18]

结合前述的约束多项式，我们可以对t(x)中出现的每一项都构建一个承诺，以实现验证方的验证。PLONK证明的具体内容如下，包含了两个点处的验证：Wz(X)为多个多项式的同点承诺，Wzw(X)则为另一个点处的对z(X)的承诺。

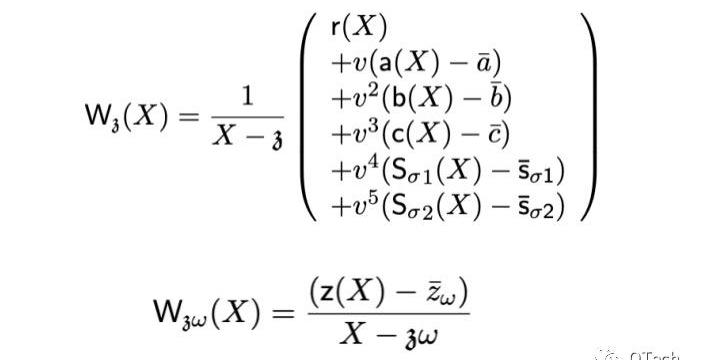
最后，PLONK的验证在原文中也被归纳为一个简洁的公式，实际上就是将上面提到的两个点处的承诺简单相加，具体等式如下所示：

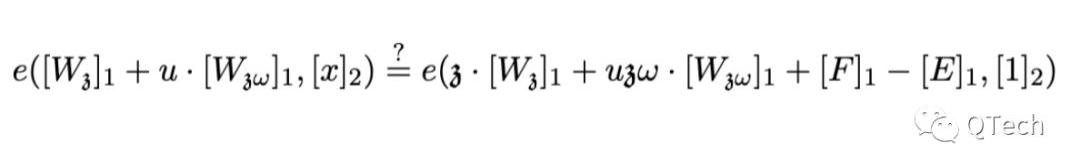
以上就是PLONK和Groth16算法内容的具体对比结果，讲了这么多冗长的公式变换，两者在性能层面的差距究竟如何呢？

性能比较

在这里我们给出的是PLONK论文中的结论。Table1是在证明阶段的一个性能比较，Table2则是验证阶段的性能。可以看出，在验证上，两者的差距不大，Groth16比PLONK多了一次配对运算；而在证明方面我们遗憾地发现，Groth16不论在证明的工作量还是证明长度上仍然保持着最优的性能。但需要指出的是PLONK，尤其当它工作在fast模式时，所使用的SRS长度是所有算法中最短的。

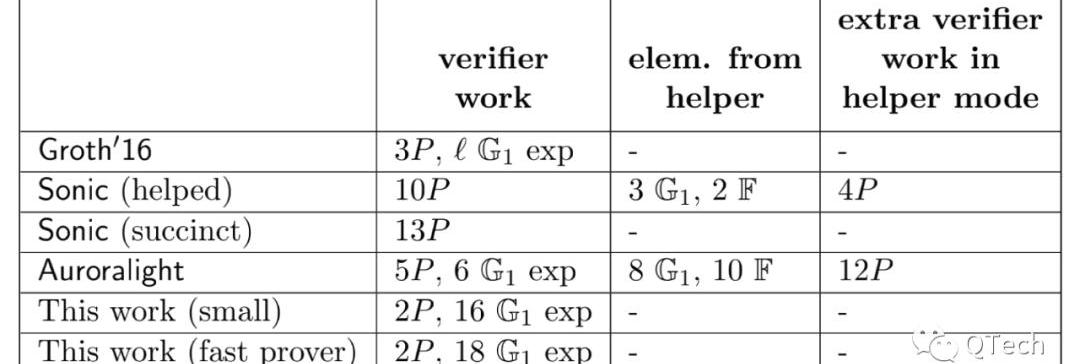
▲验证阶段性能比较

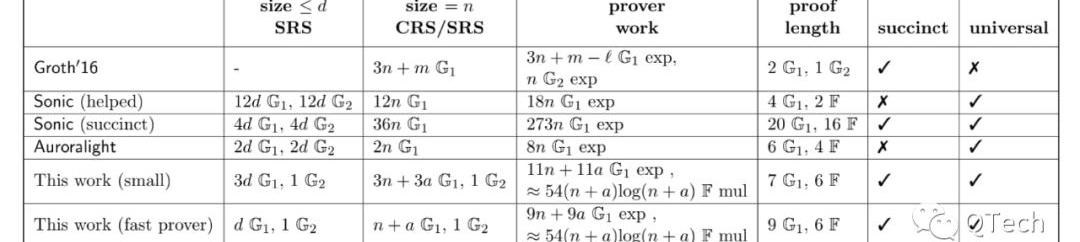
▲证明阶段性能比较

前置知识

多项式减除

顾名思义，化减为除：若我们需要证明一个多项式f(x)在点a的取值为b，也就是证明f(a)-b=0；那么我们可以将其转换为证明多项式f(x)-b可以整除(x-a)。其数学表示：

设多项式f(x)且f(a)=b，则存在一个多项式g(x)，使得：f(x)-b=g(x)(x-a)

kate承诺Kate承诺是由Kate，Zaverucha和Goldberg在2010年提出的一种多项式承诺方案。Kate承诺有多种形式，本文仅介绍PLONK中使用的常用形式，详细可参考其paper中的相应内容。其常用形式可以概括为对多项式的隐藏和部分打开验证。针对多项式f(x)，Kate承诺的具体步骤如下：

1）构造f(x)在点a处的承诺C

C：f(a)

2）选取点z，执行f(z)的opening

gz(x)=f(x)-f(z)/x-z

wz=gz(x)

3）给定f(z),C和Wz，验证Kate承诺

C=wz*(a-z)+f(z)

以上就是“PLONKVSGroth16”的全部内容，如有任何疑问，欢迎添加小助手桔子加入技术交流群，在这里，你想知道的都会得到解答～

A.Kate,G.M.Zaverucha,andI.Goldberg.Constant-sizecommitmentstopolynomialsandtheirapplications.pages177–194,2010.

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.2019.

标签：PLOLONGROROTUPLOAD价格tokenlon币有价值吗growth Root TokenOnomy Protocol

狗狗币热门资讯