MOD:密码专栏 | 动手计算双线性对（下）

前言

上一篇文章中，我们在"F_101"上找到了17个点满足椭圆曲线方程，他们构成一个循环。那么在"F_101"中元素作为坐标的点中还有没有其他的点也满足方程呢？换句话说，上篇文章列出的17个点是不是就是满足方程的全部的解呢？并非如此，比如可以验证(3,38)也满足椭圆曲线的方程，但是他不是上面17个点中的一个。另一个子群

实际上，我们甚至可以通过将(6,44)作为生成元来得到一个102个元素的循环群，这个循环群涵盖了曲线在"F_101"上的全部点。但是，曲线在"F_101"上的循环周期为17的循环群却只有中篇列出的一个，也就是说在"F_101"上讨论的话，循环周期为17的点已经被我们全部找到了。

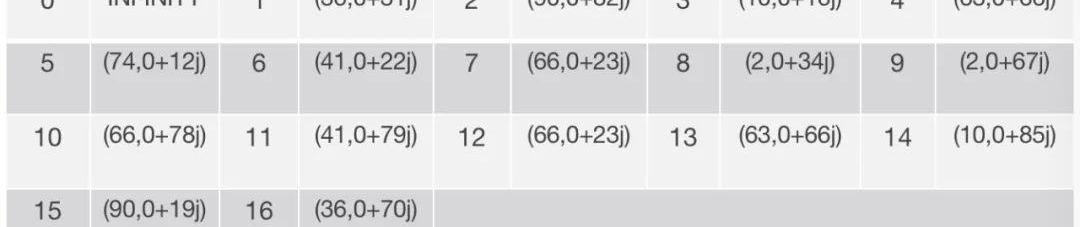
在中篇中，我们也提到数域的扩张会直接影响我们需要讨论的点的多少，那么如果我们对"F_101"进行扩张，是否能够得到更多的循环周期为17的点呢？METASTATE的博客中给出这样一个例子，我们将用这个例子说明这个命题的真假。首先我们选择满足j^2mod17=15的j用于对"F_101"的扩张，过程就像我们上一篇文章中进行的那样，扩张后的域记为“F_101的二次扩域”。在这个扩张下，我们可以找到另一个循环周期为17的群，下面的表格列出这个群的全部元素：

密码专家认定“澳本聪”最新密码主张是无稽之谈:在过去四年中，“澳本聪”克雷格·怀特（Craig Wright）一直在证明自己就是中本聪，但是根据业内密码学专家评估，克雷格·怀特最近关于比特币消息签名是如何工作说法是完全错误的。此前一位匿名用户使用相同密钥签署145个公开消息，并断言克雷格·怀特没有用于签署相关信息的密钥。然而在REIMAGINE 2020虚拟会议上，克雷格·怀特认为“没有任何消息被签名，因为你不能拥有匿名数字签名，你可以运行数字签名算法，但不是在签名消息。所以要么必须具有身份属性，要么必须具有身份才能签名消息。你不能说‘嘿，我有密钥，我正在签名’，如果有这种想法意味着根本没有理解数字签名意义。”Symbolical Software应用密码学家Nadim Kobeissi表示，对克雷格·怀特表述感到非常惊讶，因为数字签名使用确实是正确的，而克雷格·怀特所所谓'这不是数字签名工作方式'的主张似乎含糊且存在误导。约翰·霍普金斯大学副教授兼密码学家Johns Hopkins也认为，克雷格·怀特的表述对密码学家来说毫无意义，简直是胡说八道。（coindesk）[2020/7/24]

央行：坚定不移推动金融领域密码应用:中国人民银行官方公众号4月15日发布文章《学习密码法 筑牢安全防线》，强调金融室国家重要的核心竞争力，密码是保障金融网络安全，促进资金融通、加强金融监管，以及支撑金融创新的关键技术和有效途径。密码在金融领域应用广泛，比如“数字签名”护航刷卡消费、商业密码助力网上银行转账。2020年是《中华人民共和国密码法》施行元年，也是密码工作创建90周年。中国人民银行提出六点要求：

1、提高站位坚决落实：坚定不移地推进金融领域密码应用，把各项部署落到实处；

2、规划引领战略融合：加强顶层设计和沟通协调，形成指导密码应用的发展规划；

3、顺应形势创新驱动：坚持问题导向，推动创新链、产业链、价值链的整合，实施密码优先发展战略；

4、分类施策全面推进：构建金融基础设施密码支撑体系，扩大金融领域的密码应用。

5、依法管理强化评估：加强金融行业密码应用的政策和标准制定，抓好密码应用安全性评估；

6、统筹推进形成合力：推动金融领域密码全面规范应用，建立健全金融领域网络密码保障体系。[2020/4/15]

我们随机选择(66,0+23j)这个元素来验证其满足曲线方程：

动态 | EOS在CoinMarketCap基本密码资产评分中排名第一:据引力观察消息，Coinmarketcap在他们的网站上添加了基本密码资产评分(FCAS)。FCAS是度量加密货币项目健康状况。EOS目前在FCAS排名第一，915分，其次是ETH和BTC。[2019/3/21]

左侧：y^2mod101=^2mod101=23×15mod101=42

右侧：x^3+3mod101=41^3=3mod101=42

左侧等于右侧，验证完毕。

在发现通过域扩张后还能找到更多的17阶点后，我们不禁会想：

继续对”F_101的二次扩域”进行扩张，能否找到更多的17阶点呢？

或者是：为了找到全部的17阶点，我们需要对F_101进行几次扩张呢？

嵌入度其实就是描述这个问题的一个概念。E是定义在F_101上的椭圆曲线，我们已经有一个包含n=17个点的子群，我们称这个子群的嵌入度是满足17整除q^k-1的最小的k。在这个例子中，k=2。计算嵌入度的价值在于事实证明，当对F_101进行扩张以期其上的椭圆曲线包含全部17阶点时，最小的扩张次数就等于嵌入度。也就是说在”F_101的二次扩域”上，我们已经找到全部的17阶元素。

美国国家标准和技术研究所的研究人员宣布 密码学中随机数的方面出现突破:美国国家标准和技术研究所的研究人员最近宣布，在密码学最重要的一个“随机数的产生”方面取得了突破。这种实验性的新技术可能会对网络安全产生巨大影响。在以电子方式运行现代世界的“1”和“0”的数字面纱后面，随机数字每天都要在加密过程中进行数千亿次的排序，这些过程通过不断扩大的互联网为全球提供数据。[2018/4/19]

Millier循环

下面给出计算双线性映射的Millier算法，当计算e(P,Q)时，该算法根据P的坐标创建一个二元多项式，然后将P坐标的x和y分量带入求值：

METASTATE的博客中作者已经计算了e((1,2),(90,82u))点的结果为97+89j。我们给出另外一个计算的例子，并且稍后通过对比这两个例子的结果说明双线性对的一些属性。

V神回应EOS创始人对其使用经济激励和密码学来治理社区言论的质疑:4月1日，Vitalik发文回应经济激励和密码学来治理社区言论的质疑，V神表示：

1.希望创造一些工具，供至少2/3的诚实竞争团队使用。但这2/3的人是诚实的不等于2/3的资本是诚实的。

2.靠思想来竞争的社区将比购买选票的社区更有竞争力。

3.不过现在的情况不可能“证明”个人的经济风险，因为他们可能比内部人员有更多的获益或损失。

4.密码学永远无法证明的事就是审查制度。[2018/4/2]

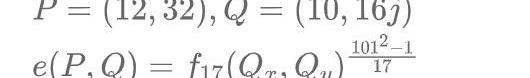
其中f_17是二元的多项式，通过一个称为Millier循环的过程我们可以生成该多项式，这个过程类似于计算指数运算时的mul-and-square操作。但是为了更直观的展示原理，我们选择根据上文定义直接展开计算f_17，这会增加一些计算量。

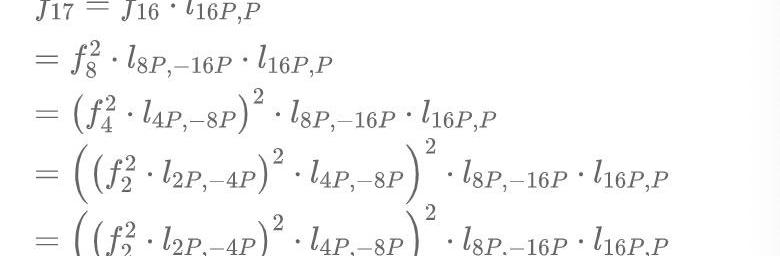
因此我们需要计算

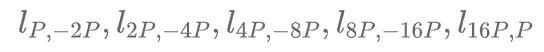
的表达式。通过查询上一篇文章的列表我们可以找出P，±2P，±4P，±8P,±16P的值,其中P=(12，32)=5G：

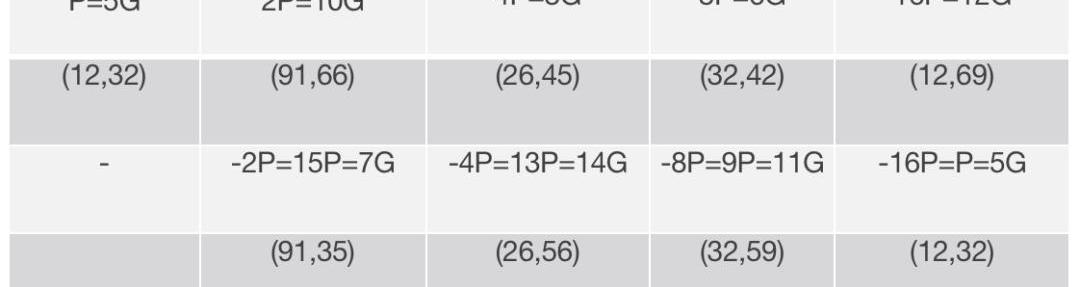
接下来我们来计算这些直线的方程：

这样我们已经可以计算f_17的结果：

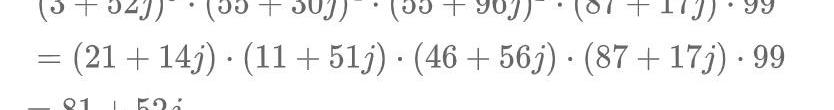
最后我们计算(81+52j)^600

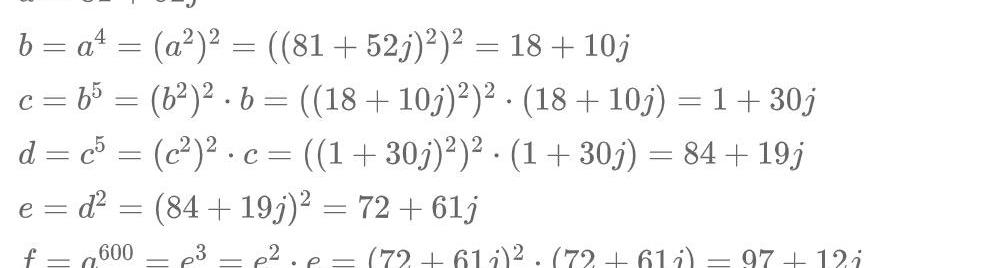
完全解决curve101配对问题

实际上，我们可以计算出GT的生成元e(G1,G2)，也就是e((1,2),(36,31j))，其值为7+28j。这样我们能够完全掌握GT中全部的元素：

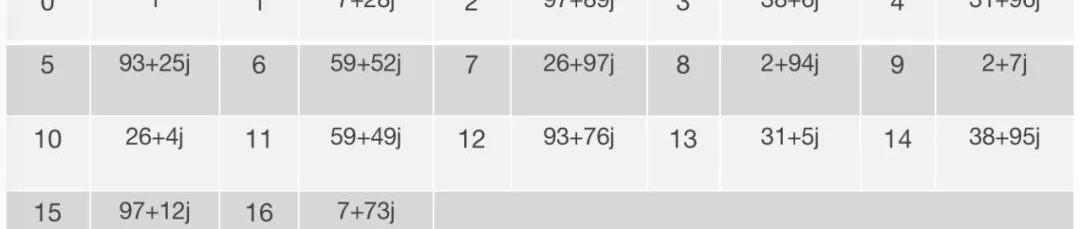
可以看到GT也是一个循环群，他其实是在“F_101的二次扩域”上满足方程x^17=1的17个根。根据该表我们不加以计算就可以知道这个配对的任何一个计算结果，例如e((12,32),(36,31u))=e(5G1,G2),因此其值就是上表的第5个元素：93+25j。我们之所以能够完全解决curve101的配对问题，是因为curve101的一系列参数决定其足够简单，而实际零知识证明算法中使用的配对就要复杂很多。例如一些标准中要求其配对曲线的嵌入度至少为12，这意味着GT的元素至少是基础素域的12次扩张！如果其素域特征为常见的256位，那么为了表示一个GT元素就需要256*12/8=384字节的大小。对于任何一个实际使用的曲线，其计算复杂度和规模都使我们当前绝无可能计算出其映射表，这也是离散对数问题困难的所在。

通过系列文章，我们计算了一个简单的配对曲线，加深了对双线性映射的理解。后续，我们继续使用这个配对曲线来讲解和演示零知识证明中Groth16算法的过程和原理，敬请期待。

乔沛杨趣链科技基础平台区块链底层密码学小组

标签：MODCASCURMILmod币圈是什么意思bMeme CashCurveMILF价格

DOT热门资讯