ACA:你可能不知道隐藏在杨辉三角形中的 10 个秘密！

文章来源于遇见数学，作者遇见数学翻译小组

翻译:姚高华校对:李千蔚

英文:https://sourl.cn/qZZiVA

杨辉三角形，又称帕斯卡三角形、贾宪三角形、海亚姆三角形，它的排列形如三角形。因为首现于南宋杨辉的《详解九章算法》得名，而书中杨辉说明是引自贾宪的《释锁算书》，故又名贾宪三角形。古代波斯数学家欧玛尔·海亚姆也描述过这个三角形。在欧洲，因为法国数学家布莱兹帕斯卡在1653年的《论算术三角》中首次完整论述了这个三角形，故也被称作帕斯卡三角(Pascal'striangle)。

杨辉三角的前10行写出来如下：

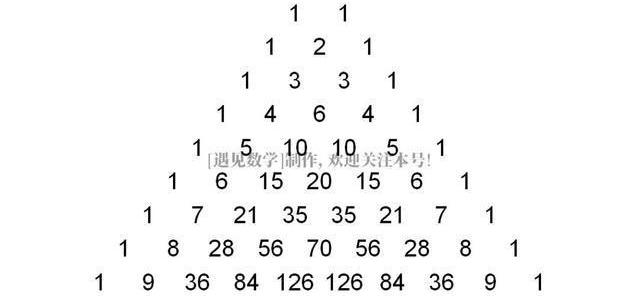
杨辉三角的构建

在最上面一行的中央写下数字1第二行，写下两个1，和上一行形成三角形随后的每一行，开头和最后的数字都是1，其他的每个数都是它左上方和右上方的数之和，就是说除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和。

意大利央行：稳定币根本没有被证明是稳定的:金色财经报道，意大利央行在一份研究报告中报告也强调需要平衡监管与创新，报告称，加密货币寒冬的后果为政策干预提供了更明确的理由，并非所有加密活动和所有形式的加密资产都需要涵盖或应该受到金融部门监管，特别是当其发行、交易和持有不通过支付或投资功能满足客户的财务需求时。银行官员称权力下放确实难以捉摸，常常是一种幻想，但有时却是现实，可能会成为长期存在的创业形式的替代品。事实上，稳定币有时被描述为跨境支付市场上的有效替代品并没有被证明是稳定的。

央行还称，我们还观察到，从市场角度来看，这些资产的表现越来越像传统资产。[2023/6/29 22:07:12]

左对齐后的杨辉三角

前两列倒没什么特别的地方，第一列均为1，第二列则为自然数。而第三列就是三角形数(Triangularnumber)。你可以想到，三角数就是能够组成大大小小等边三角形的点的数目，如下图所示。

Vitalik Buterin：在以太坊上重新质押时需谨慎:金色财经报道，以太坊联合创始人Vitalik Buterin表达了对以太坊共识机制超出其原始设计的过度复杂化的担忧，特别是在重签方面，重签是Eigen Layer等公司正在开发的一种机制，它扩大了以太坊验证者的责任，包括确保外部链的安全。他担心，重新锁定可能会引入影响网络安全的风险。Vitalik Buterin表示，在以太坊上重新质押时需谨慎。[2023/5/22 15:18:50]

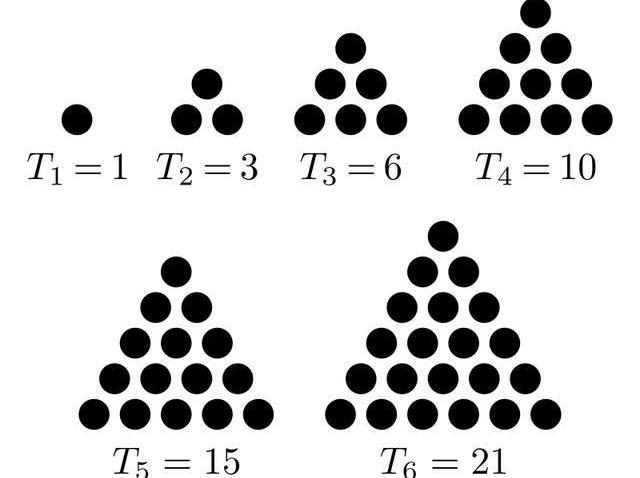
三角形数(图自维基)

类似地，第四列是四面体数(Tetrahedralnumber)，也叫三角锥体数。顾名思义，它们代表由三角形构成的四面体所需要的点的数目，四面体数每层为三角形数。

FTX Japan发布客户资产管理状况报告，公司持有余额超过客户存入资产:11月14日消息，FTX旗下日本加密衍生品交易所FTX Japan今日凌晨在官网上披露了客户资产管理情况。在其支持的14种加密货币均存入公司的冷钱包中，冷钱包存有的加密货币余额均大于客户在该平台存入的资金余额。此外，公司持有的法定货币（日元和美元）余额超过客户存入的法币资产，余额约2.78亿日元（约合200万美元）。

FTX Japan还公布了自有资产状况，称公司净资产约100亿日元（截至2022年9月，约合7186万美元），现金和存款约196亿日元（截至2022年11月10日，约合1.41亿美元）。

此前11月10日消息，日本金融厅命令FTX Japan在12月9日之前停止运营，并要求其在11月16日之前披露客户资产保护信息。[2022/11/14 13:01:31]

Acala：黑客攻击系iBTC/aUSD池配置错误，相关被盗资产已被禁止转移:8月14日消息，Acala发推表示，此前的黑客攻击系iBTC/aUSD流动性池的配置错误，导致大量aUSD的错误开采。该配置错误已被纠正，收到错误铸造的aUSD的钱包地址已被确定，Acala正在对这些地址进行链上活动追踪。

据初步的链上追踪显示，99%以上错误铸造的aUSD仍在Acala平行链上，被兑换为ACA或其他Token。在Acala社区集体治理决定如何解决错误铸币之前，留在Acala平行链上的这些错误铸造的aUSD及其兑换Token将被禁止转移。[2022/8/14 12:24:51]

图自维基

秘密Billions项目组3：11的幂

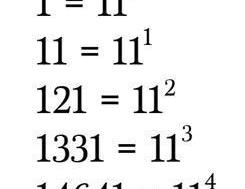
供应链：显卡2022年出货量跌幅或高达2-3成:7月6日消息，据PC供应链表示，由于挖矿热潮消退，显卡2022年出货跌幅高达2-3成，显卡呈现价量齐跌走势，从英伟达、AMD、英特尔，到板卡、相关芯片等供应链影响甚巨。（金十）[2022/7/6 1:53:50]

杨辉三角还揭示了11为底的幂的值。你要做的就是将每一行的数字挤压到一起。前5行足够简单，但出现两位数的时候该怎么办呢？

事实证明，你要做的就是将十位数加到它左侧数字上，比如下图所示的是第六行中出现了上面的情况，如何进行移动以获得11的值

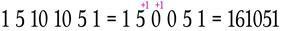
如果出现了三位数同样进位处理即可。

秘密Billions项目组5:斐波那契数列

为了揭示隐藏的斐波那契数列，将左对齐的杨辉三角对角线相加。比如下图杨辉三角中发现的斐波那契数列前九个数：1，1，2，3，5，8，13，21，34…

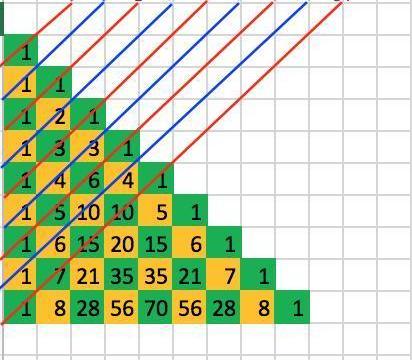
按线条所示相加结果即为斐波那契数列(图自维基)

秘密Billions项目组7:组合数学

或许杨辉三角中发现的最有趣的关系就是我们如何利用它找到组合数。

杨辉三角的前六行写成组合数的表达形式

回忆一下从n个不同元素中选k个元素的组合公式。我们发现，对于杨辉三角中的每一行数字，从零开始计数，n是行数，k是在这一行中的位置。

所以，如果你想计算4选2，看第5行，第3个数，你会发现，答案是6.

秘密Billions项目组9:二项式定理

(x+y)的幂运算是很酷，但我们多久才会需要解这样的题呢？很有可能，不太经常需要。如果我们能够从上一个章节的结论中总结出一个更有用的形式，会不会更方便？好吧，其实这就是二项式定理：

这个公式也称二项式公式或二项恒等式。

秘密#10:与概率之间的联系—二项式分布

二项式分布描述了具有两种可能结果的实验的概率分布。事实上，杨辉三角的每一行也能揭示了这样的清晰，以最经典就是扔一枚硬币为例吧。

如果考虑抛3次硬币，就会有8种可能发生的事件：

但其实可以分为4类情况：

3次反面——只有1次发生2次正面和1次反面——有3次发生2次反面和1次正面——有3次发生3次正面——只有1次发生这注意1,3,3,1正是杨辉三角的第4行。同样如果抛5次硬币，出现3正2反的事情会出现10次，这也是出现在了杨辉三角第6行。

如果设抛硬币得到正面概率为p，反面概率为1–p。想知道扔到正面的可能性，我们可以使用二项式分布的概率质量函数找到概率的分布，其中n是试验次数，k是成功次数。

二项式分布的概率质量函数

嗨，这看起很熟悉啊！这几乎和我们前面提到的二项式定理是一样的公式，只是没有求和公式，同时和被和代替了。

假设成功的概率是0.5(p=0.5)，我们计算扔到正面0次、1次、2次、3次的概率。

在公式中代入n=3、k=0,1,2,3，得到下面计算结果，请注意杨辉三角里的组合数：1,3,3,1：

扔到正面0次、3次的可能性都是12.5%，而扔到正面1次、2次的可能性都是37.5%，这与上面分析结果是一致的。

这便是看似简单的杨辉三角里的10个秘密，是不是很精彩啊！但这并非终点，它还有另外更神奇的性质隐藏其中，等待我们未来继续探索吧。

来源：遇见数学

编辑：他和猫

↓点击标题即可查看↓

1.套娃吗？你先看这个岛中湖中岛中湖中岛

2.都靠这位天才科学家20岁时的论文，你才能用手机拍照发朋友圈

3.朝天空开，子弹掉下来还有杀伤力吗？|No.206

4.乐高还能悬浮在半空中？上百万人已看懵！

5.古装片的射箭动作把物理学家看笑了，导演咱能不能专业点？

6.即使被它淹没也不会窒息，这是什么神奇液体？

7.数学课上捡了个橡皮，勾股定理就看不懂了

8.物理学写给你的情书

9.唯一两次获得诺贝物理学奖的人，你却不一定认识他

10.妈妈问我的桌子为什么这么乱！

标签：ACACALALAUSDMetaRacacarVerticaldecentraland币价格btc价格今日行情usdt

USDT热门资讯