作者:?LeoWhitehead
翻译&校对:?IANLIU?&阿剑
来源:以太坊爱好者
-广受欢迎的加密通讯工具——OpenSSL,其中的部分代码-
关于密码学的内在原理,一直被认为是少数专家或数学家才能涉足的领域,其中的技术细节在大多数人看来就像变魔术一样。考虑到现代密码学的复杂程度,我们可以理解为什么很多人对密码学存在这些误解;但不了解密码学,可能会做出很多弊大于利的决定,比如英国的加密禁令提案,澳大利亚的援助和访问法案等。
在本篇指南中,我们会帮助大家掌握学习密码学所需的入门知识、对不同密码学体系的发展历程进行简介,并对当前三个最流行的密码学领域——流密码、分组密码、公钥密码,进行快速上手指导。
密码
“密码”指的是对消息进行加密或解密的算法,也是密码学的基石。加密算法(E)使用密钥(k)对消息(m)进行加密,并生成密文(c);类似地,解密算法(D)使用密钥(k),对密文(c)进行解密。如下列所示:
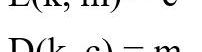
-加密算法'E'及解密算法'D'-
上述过程也意味着,一种算法要想被称为“密码”,还必须满足以下的一致性方程特性,确保密文可以被解密。
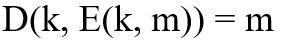
式子表明着如果你使用密钥?K?对消息进行加密,也能使用密钥?K?对密文进行解密,并得到与原来消息一摸一样的输出。
人大附中物理老师李永乐科普拜占庭将军问题和区块链:5月14日,人大附中物理老师、科普视频网红李永乐在其公众号发布视频《拜占庭将军问题是什么?区块链如何防范恶意节点?》。李永乐老师在视频中对拜占庭将军问题和区块链进行了讲解,他表示,拜占庭将军问题本质上指的是,在分布式计算机网络中,如果存在故障和恶意节点,是否能够保持正常节点的网络一致性问题。在近40年的时间里,人们提出了许多方案解决这一问题,称为拜占庭容错法。例如兰波特自己提出了口头协议、书面协议法,后来有人提出了实用拜占庭容错PBFT算法,在2008年,中本聪发明比特币后,人们又设想了通过区块链的方法解决这一问题。区块链通过算力证明来保持账本的一致性,也就是必须计算数学题,才能得到记账的权力,其他人对这个记账结果进行验证,如果是对的,就认可你的结果。与拜占庭问题比起来,就增加了叛徒的成本。[2020/5/14]
其中一种最古老、最简单的密码就是凯撒密码——直接从字母表中选取特定位置,替换掉原消息中的字符。
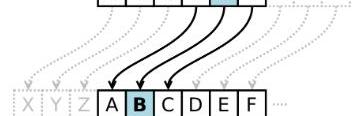
-凯撒密码出现于公元50年,凯撒大帝使用字母表跳三位的字来替换原来的消息内容,用于军事通讯-
下面的例子就是经过后三位字符替换过后的密文形式:
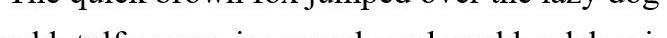
凯撒密码可以用下列式子表示:

虽然这种做法符合我们对密码的定义,但是它非常不安全。只要攻击者知道密文是以这种方式加密,就能通过尝试另外25种组合进行破译;即使攻击者不知道密文使用了凯撒密码,他们也能够观察到密文中的规律进行破译。
动态 | 人民日报官方微博科普区块链 强调区块链不等于比特币:人民日报官方微博今早发表9图科普区块链。其中涉及区块链的特点有:1、安全;2、不可篡改;3、可访问;4、无第三方。区块链对未来的影响:1、不需繁琐个人证明;2、看病避免反复检查;3、旅行消费更加便捷;4、交易无需第三方。同时强调,区块链不等于比特币。比特币只是区块链技术的一种应用,区块链还有医疗卫生、食品安全、版权保护等诸多应用领域。[2019/10/28]
虽然这种做法符合我们对密码的定义,但是它非常不安全。只要攻击者知道密文是以这种方式加密,就能通过尝试另外25种组合进行破译;即使攻击者不知道密文使用了凯撒密码,他们也能够观察到密文中的规律进行破译。
在进一步介绍更安全的加密算法之前,我们得先聊聊什么是Xor运算。
XOR
Xor运算,又称为“异或门”,是一种布尔变量逻辑判断,能接收1或0作为输入:如果输出1则表示两个输入不同;输出0则表示两个输入相同。下图的真值表列出了经过异或运算后,所有可能的输入输出组合:
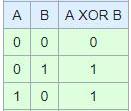
异或运算也经常用符号⊕来表示:
0⊕0=0
0⊕1=1
1⊕0=1
1⊕1=0
关于异或逻辑,以下有几点重要的特性:
异或运算结合律:a⊕(b⊕c)=(a⊕b)⊕c
对自身进行异或运算结果为0:a⊕a=0
对0求异或,结果为自身:a⊕0=a
根据上述异或运算的规则,我们知道a⊕b⊕a等同于a⊕a⊕b,也等于0⊕b,运算结果为b。要注意的是,这些异或运算特性只适用在1和0,因此对不同进制的数字进行异或运算之前,需要先将其转换为二进制。例如:
87⊕73=1010111b⊕1001001b=0011110b=30
动态 | 币安科普MimbleWimble算法:币安官方推特今日发布隐私算法Mimblewimble的科普贴,在下方留言区大量网友留言猜测是否是基于 Mimblewimble算法的隐私币Grin或者Beam即将登陆币安交易所,其中猜测Grin的呼声更高。[2019/9/2]
接着,我们可以开始介绍第一种安全密码了。
一次性密码
FrankMiller在1882年提出了一次性密码的概念——加密:将消息和私钥进行异或运算得到密文;解密:将密钥和密文进行异或运算得到原消息,这个过程类似于前面提到的a⊕b⊕a=b。一次性密码的定义如下所示:
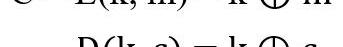
该密码的一致性方程也很容易证明:

一次性密码非常容易上手,假设我们要加密一串字段“Message”,首先可以通过ASCII字符集将“Message”转换为二进制数据。

现在,我们需要一组56位随机二进制数来对明文进行异或运算,该私钥随机程度越高越好!
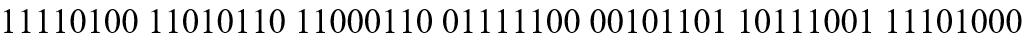
-从random.org生成的随机数-
我们将明文和私钥的每一位进行异或运算。
动态 | 浙江卫视节目科普支付宝区块链防伪溯源产品:昨日,在浙江卫视播出的科普综艺栏目《智造将来》现场,支付宝首次展示了支付宝区块链防伪溯源产品,以接地气的方式公开向大众展示区块链在生活中的应用。[2019/3/4]

运算后的结果就是我们的密文了!要解开密文也很简单,我们只需要将密文和刚才生成的私钥进行异或运算,并转码回ASCII,就能得到原消息。

这种密码简单易用,而且还有个很有意思的特点。一次性密码具有所谓的完全保密性,这意味着从数学角度来说,攻击者不可能从密文推得任何原消息的内容,当然也不可能破译。
既然我们已经有了简单易用,且不可能破译的密码,为什么我们还会想用其他的密码呢?根本原因在于,一次性密码虽然很有效,但是他有一些重大的缺陷。
第一个缺陷是,不论我们想要加密什么样的消息,都需要有和原消息一样长或是更长的私钥用于加解密。而且为了让密文接收者能够解密密文,需要有绝对安全的通信方法把私钥给到接收者;这就形成一个悖论,如果有这种安全通道,那不如直接把原消息发过去得了。
第二个缺陷可以从“一次性密码”的名称中发现。针对不同消息,同一个私钥每回只能使用一次;如果对多个消息重复使用同一个私钥,其引发的问题可以从数学推导上看出。
假设我们有两条消息m1和m2,分别使用相同的私钥k进行加密。通过异或运算,我们会得到以下密文:
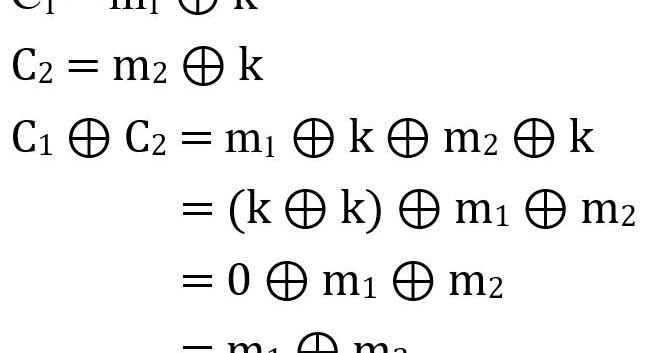
科普时报:区块链与云计算长期发展目标不谋而合:据《科普时报》今日报道,区块链与云计算两项技术的结合,从宏观上来说,一方面,利用云计算已有的基础服务设施或根据实际需求做相应改变,实现开发应用流程加速,满足未来区块链生态系统中初创企业、学术机构、开源机构、联盟和金融等机构对区块链应用的需求。另一方面,对于云计算来说,“可信、可靠、可控制”被认为是云计算发展必须要翻越的“三座山”,而区块链技术以去中心化、匿名性,以及数据不可篡改为主要特征,与云计算长期发展目标不谋而合。[2018/5/4]
从上图,我们可以从密文C1⊕C2得到m1⊕m2。对于攻击者来说,他们就能基于这种关联性,通过各种统计分析、频率分析、模式匹配,或是使用2006年提出的自然语言处理方法,来获得原消息的内容。我不会深入解释存在这种关联性具体造成的危害,这里只是形象的说明当同一个私钥被使用的次数越多,密码的安全性就越低。
现在我们已经具备XOR加密和一次性密码的基础知识,是时候了解其他更实用的加密方法了。
流密码
一次性密码具有非常好的安全性,这意味着手上只有密文的情况下,攻击者不可能进行破译。但是好的安全性基于长度大于等于原消息的私钥,这使得一次性密码并不实用,因为如果加解密双方有很好的方法来传递消息和私钥,他们直接传递消息就好,没必要进行加密。
为了让一次性密码更加实用,我们引入“流密码”的概念。流密码的核心思想是——以“伪随机”密钥替代一次性密码中的“随机”密钥,伪随机密钥产生自
密码学安全伪随机数生成器。要注意的是,CSPRNG不同于一般的伪随机数生成器,因为CSPRNG产生的数据必须和真实随机数看起来没有区别才行。CSPRNG是一种算法,能产生一长串数字,类似于随机数的性质。因为随机数很难生成,所以CSPRNG要依靠种子来决定初始状态及将来产生的数;CSPRNG从相对较小的起始种子生成海量的随机数。如果起始种子是已知的,则随后产生的所有数都是已知的,也就是说CSPRNG具有确定性;这也导致CSPRNG产生的数,其随机程度完全取决于种子的随机程度。为了让一次性密码更加实用,我们可以根据所需长度,使用伪随机数生成器的输出替换原来的私钥;这样的话只要传递初始种子就可以了。因为CPRNG具有确定性,使用相同种子能得到相同输出。
为了更好理解,我们先看看原来的一次性密码:
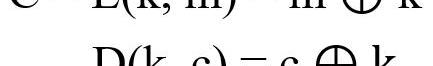
使用伪随机数生成器的输出G(K),替换原来的私钥K:
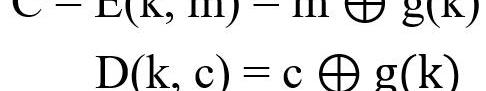
替换后的私钥可以远远短于要加密的消息,使得分配及管理私钥更为方便,进一步改善了一次性密码不实用的问题。但这种做法也带来了新的问题:
将原来完全随机的私钥替换为安全随机数生成器的输出,会导致私钥长度比原消息短,使得我们的密码不再具有完全保密性。因此流密码的安全性取决于我们的伪随机数生成器的不可预测性。如果可以预测CSPRNG的输出,则可以获得明文消息。以下是大家熟知的一些使用弱流密码的密码系统:
802.11bWEP:WEP是一种给WiFi数据做加密的算法,它使用的流密码称为RC4。因为流密码中不能一直使用同个密钥,所以长期使用的密钥包含一个每次都会变动的值“IV”;然而“IV”只有24位,也就是说加密超过5000条消息后,就会有五成的概率出现相同的密钥。
CSS:DVDForum使用内容扰乱系统来管理DVD的数字版权,使得仅有获得授权的应用才能访问DVD内容。CSS使用40位的密钥,而40位的密钥空间较小,可以相对快速地暴力破解。
现在我们也掌握了流密码的知识,可以进一步讨论下一个密码系统——分组密码。
分组密码
分组密码是另一种能用于加解密数据的方法。分组密码包含两种算法:E用于加密,D用于解密,同时也用到了密钥K。

分组密码的核心在于,要加密的明文和输出的密文长度始终相同,为一固定量。该固定量称为“blocksize”,大小取决于所使用的分组密码算法。另外,私钥K的长度被称为密钥大小,也是固定量。常见的两种分组密码分别是3DES及AES——3DES具有64位的消息大小和168位的密钥;AES具有128位的消息大小和128、192或256位的密钥。
因为分组密码把可能的区块映射到其他的每一个区块,所以也被称为“用密钥完成的置换”或是“伪随机置换”。非常重要的一点是,私钥决定了输入的区块和相关密文区块的映射关系,而且是一对一排列的,所以只要知道私钥就能解密密文。
第一个比较重要的分组密码是1970年代IBM开发的数据加密标准,但DES并不安全,很快就被3DES取代;紧接着3DES又被1997年开发的高级加密标准所取代。AES是在国家标准与技术研究所的要求下制定的标准化分组密码。AES是当今使用的最常见的分组密码,重要性大大超过DES和3DES,所以我将着重介绍AES。
在我解释AES到底是怎么运作之前,先提醒一下我会跳过很多技术细节,如果有人对这深入这方面领域有兴趣,可以从这里获得你想要的。
AES及大部分分组密码,都是通过迭代进行运作的,输入的文本消息会使用连续的密钥以迭代的方式进行加密。第一步是获得一个密钥K,密钥一般是128位、192位或256位的,在这里我们只演示128位的AES;然后拿该密钥推导出一系列的RoundKeys来加密我们的消息。
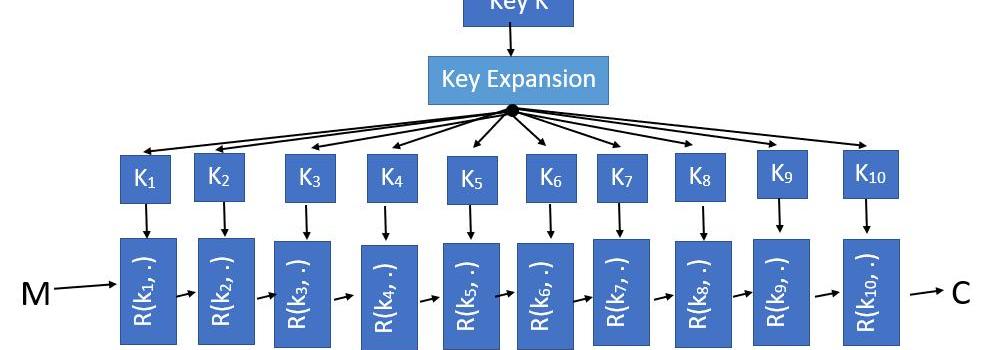
上图例子中,我们输入128位的密钥,并通过Rijndael密钥方法?将密钥扩展成11个16字节的子密钥。接着,AES将原消息放入轮次函数?R(kn?,m)?进行独立加密计算,每次计算把扩展出来的轮次密钥?kn?及消息状态?m?作为输入,总共进行10次。
因为AES只能用在128位的消息上,因此我们把输入的消息?m?表示成4x4矩阵的单字节单元,同时也能把轮次密钥表示成4x4的矩阵,这样就可以对消息及其中间状态进行异或运算了。

首先,输入的消息和第一个轮次密钥进行XOR,再通过字节替代、行位移、列混淆等运算,输出转变后的消息状态作为结果。接着我们使用不同的轮次密钥重复上述这些步骤10次,唯一的不同点在于最后一次的计算不包含列混淆。最终的消息状态和第十一个轮次密钥进行异或计算,得到最后的输出。下面简述了每一轮次的计算中包含的三种步骤:
字节替代:根据替换表,将消息状态矩阵中的每一个字节,替换为相应的字节。
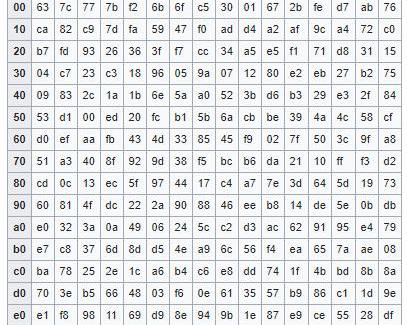
-在AES使用的替换表中,每一个字节单元以16进制表示。如,字节9a会替换为b8-
行位移:定量移动每一行。第一行不移动,第二行左移一位,第三行左移两位,第四行左移三位。
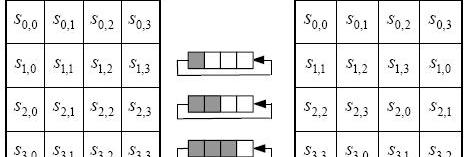
列混淆:对消息状态中每一列进行线性变换。目前为止,我们已经能使用AES来加密数据。然而,你可能很快能发现AES的局限性——没办法在只用一次AES的情况下,对超过128位的消息进行加密。要对超过16字节的消息进行加密,我们需要引入模式加密概念。
摘要:目前,比特币大概率结束阶段性调整,或将开启慢牛震荡行情;短时,大盘继续横盘调整,短时变盘的可能性在增加.
1900/1/1 0:00:00文|芦荟出品?|?Odaily星球日报 如火如荼的Defi之外,「隐私」正在被重提。今年8月的柏林web3.0峰会上,美国棱镜门主角爱德华?·斯诺登罕见地出现在视频连线荧屏上,在40分钟的时间里.
1900/1/1 0:00:00作者:蔡恒进,来自武汉大学计算机学院和卓尔智联研究院;汪恺,来自武汉大学计算机学院摘要:“一带一路”倡议加强了我国与多国之间的互信与经济融合.
1900/1/1 0:00:00作者:超级君矿工的春天正在悄然降临,11月6日,新闻报道发改委从“淘汰产业”名单中删除“淘汰虚拟币挖矿部分”,瞬间这条新闻成为朋友圈刷屏一景,币价也因此略有上升.
1900/1/1 0:00:00本文来自?deribit,原文作者:DerekHsue,SuZhu,Hasu&BrandonCurtisOdaily星球日报译者|Moni 在本文中.
1900/1/1 0:00:00作者:白玉盘一、关于随机数随机数,作为一种重要的基础科学资源,应用非常广泛,是密码学、博弈、科学仿真……的基础。最早对随机数的认识,是从开始.
1900/1/1 0:00:00